A Global Tree of Languages
I was a reviewer for the Evolution of Language (Evolang) conference for the first time this year, a tedious-sounding task that turned out to be hilarious. The conference attracts some bizarre manuscripts on the origins of language, one particularly imaginative one I wanted to devote a blogpost to, but regretfully cannot because of reviewer confidentiality.
Also in my inbox to review was the most exciting paper about language that I’d ever seen. I recommended acceptance obviously, even though it was only tangentially related to the theme of the conference, and it was accepted as a poster and published in the conference proceedings (available here).
The paper was by Gerhard Jäger and Søren Wichmann, about constructing a world family tree of languages using a database of basic vocabulary, the ASJP database. Claims about how language families may be related are nothing new but are normally statistically uninformed (such as work by Merritt Ruhlen and Joseph Greenberg). The amazing thing about this new paper is that it uses a simple statistical test of relatedness between languages, extending the methodology of a paper by Gerhard Jäger in PNAS last autumn and covered in my post here, and finds evidence for language families around the world being related to each other in a geographically coherent way, clustering into continents and even reflecting quite specific events in human history.
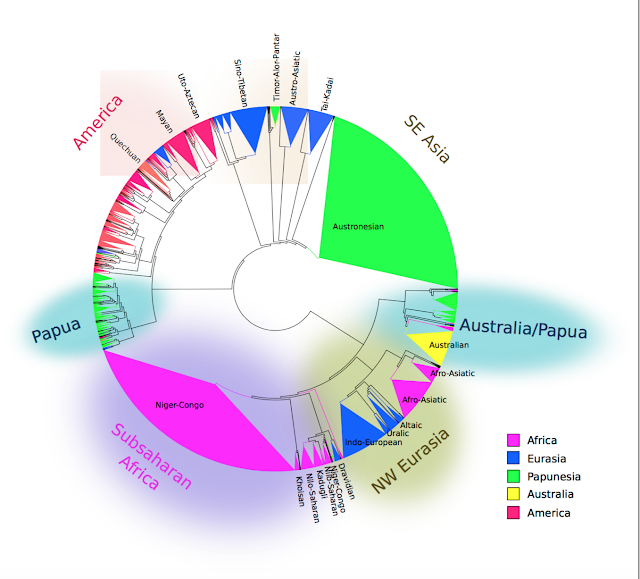
The resulting family tree of around 6000 languages and dialects was what they presented as a poster at Evolang. If correct, it might as well be on the cover of Nature:
Also in my inbox to review was the most exciting paper about language that I’d ever seen. I recommended acceptance obviously, even though it was only tangentially related to the theme of the conference, and it was accepted as a poster and published in the conference proceedings (available here).
The paper was by Gerhard Jäger and Søren Wichmann, about constructing a world family tree of languages using a database of basic vocabulary, the ASJP database. Claims about how language families may be related are nothing new but are normally statistically uninformed (such as work by Merritt Ruhlen and Joseph Greenberg). The amazing thing about this new paper is that it uses a simple statistical test of relatedness between languages, extending the methodology of a paper by Gerhard Jäger in PNAS last autumn and covered in my post here, and finds evidence for language families around the world being related to each other in a geographically coherent way, clustering into continents and even reflecting quite specific events in human history.
The resulting family tree of around 6000 languages and dialects was what they presented as a poster at Evolang. If correct, it might as well be on the cover of Nature:
I find this tree exciting because geographical patterns emerge purely out of comparing lists of words in different languages. The four lists of words below, for example, do not seem to have much in common, but somehow the algorithm manages to correctly place A and B in Papua New Guinea, and C and D in South America. (The languages are Yabiyufa, Dubu, Nadeb and Kukua).
A B C D
I: nemo no u*h we*b
one: makoko k3rowali SEt bik
blood: oladala t3ri yuw be*p
fish: lahava ambla hu*b keh
skin: upala ser buh baka7 Co
The way that the algorithm works is to calculate the distance between two word lists, namely how different two languages are. The way this is done is to take words for the same concept, and align them using an alignment algorithm. Then the difference between the words is computed using a matrix of what substitutions are most probable. For example, ‘p’ often changes to ‘f’ , as in the cognates Latin pater ‘father’ and English ‘father’. This matrix of probable sound changes can be computed using an unsupervised learning method from the data itself, by looking at only the most similar languages, such as English and Dutch, or Italian and French, and counting how many times particular phonemes are aligned with each other in these related words.
The distances between words are then summed and produce an overall measure of similarity between languages. Languages with shorter distances to each other are then placed nearer to each other in the family tree using a neighbour-joining algorithm. As expected, almost all language families that we already know about emerge from this method, such as Indo-European, Austronesian, and so on, with only a few exceptions corresponding to more controversial families. The novel part is that these known families cluster into larger groups, 'macro-families', that make sense geographically.
The word lists contain only about 100 words. The simplicity of the algorithm and the paucity of the data used make it even more surprising that a coherent result comes out (other phylogenetic studies require a few hundred words, such as work using the Austronesian Basic Vocabulary Database). The full tree is available to inspect online here. Before critiquing the methodology, I will suspend disbelief and savour some of their results.
Perhaps the most impressive result is that indigenous languages in the Americas come out as a single group. South America contains over a hundred language families, which linguists have been unable to relate to each other. This algorithm demonstrates for the first time that they have something in common, and also with the languages of Meso-America and North America, commonalities which are unlikely to be entirely due to recent contact given the distances involved and may therefore reflect events over the last 20,000 years.
The distances between words are then summed and produce an overall measure of similarity between languages. Languages with shorter distances to each other are then placed nearer to each other in the family tree using a neighbour-joining algorithm. As expected, almost all language families that we already know about emerge from this method, such as Indo-European, Austronesian, and so on, with only a few exceptions corresponding to more controversial families. The novel part is that these known families cluster into larger groups, 'macro-families', that make sense geographically.
The word lists contain only about 100 words. The simplicity of the algorithm and the paucity of the data used make it even more surprising that a coherent result comes out (other phylogenetic studies require a few hundred words, such as work using the Austronesian Basic Vocabulary Database). The full tree is available to inspect online here. Before critiquing the methodology, I will suspend disbelief and savour some of their results.
Perhaps the most impressive result is that indigenous languages in the Americas come out as a single group. South America contains over a hundred language families, which linguists have been unable to relate to each other. This algorithm demonstrates for the first time that they have something in common, and also with the languages of Meso-America and North America, commonalities which are unlikely to be entirely due to recent contact given the distances involved and may therefore reflect events over the last 20,000 years.
Similarly, languages across northern Eurasia are related in this tree. The so-called Altaic family emerges, comprising Turkic, Mongolic and Tungusic. Interestingly, Japanese and Korean are not present, despite sometimes being placed with them in the so-called 'Transeurasian' family. Martine Robbeets has a group at the MPI for the Science of Human History in Jena specifically devoted to demonstrating the validity of Transeurasian and investigating its linguistic, genetic and archeological history. For what it is worth, Japanese is placed in Jäger and Wichmann's tree next to Sino-Tibetan and Hmong-Mien (probably reflecting borrowing from Chinese); Korean is placed with the language-isolate Burushaski in Pakistan and more distantly to languages of New Guinea and Australia (implausible, although not actually impossible if all closer relatives of Korean in Asia have died out).
There is a larger ‘Nostratic’ family covering the whole of Eurasia as well, linking the Altaic languages with Indo-European, Uralic and languages of the Caucasus. The language family Afro-Asiatic is on the very outside of this family, a satisfying result because despite most branches of Afro-Asiatic being found in Africa, there is a lot of genetic and archeological evidence linking these populations with movement from Eurasia into North Africa in the last 10,000 years, as Jared Diamond among others has noted in his paper on how language families often spread with farming. There has previously been no linguistic evidence at all for a Eurasian origin of Afro-Asiatic languages, so it is very interesting that it is supported in this analysis.
In Asia, Austronesian and Tai-Kadai turn out to be related, a hypothesis long maintained by Laurent Sagart, Weera Ostapirat and others, but which has previously not been assessed statistically. Austronesian is known to have originated in Taiwan, and if it is related to Tai-Kadai, it looks like we can now push back its origins further to southern China. Further up, this Austro-Tai family turns out to be closely related to Austro-Asiatic, another southeast Asian family.
Could information about migrations over tens of thousands of years really be contained in these word lists? The paucity of the data (between 40 and 100 words per language) and the simplicity of the algorithm make these results even more remarkable. Some people may be sceptical at the very idea of being able to reconstruct language history that far back. This knee-jerk reaction is disappointingly common and mostly reflects an inability to assess statistics, such as in people's reactions to Jäger's 2015 paper on the 'eurogenes' blog:
A more reasoned approach is to look at the vocabulary similarities between languages and ask how plausible they really are. Somebody called 'Ebizur' on the same blog commented on the supposed cognates between Korean and Burushaski:
Another objection might be that language contact is partly responsible for the similarities between geographically neighbouring languages. The authors acknowledge the problem of language contact, but also say that it often does not affect the results: known instances of contact such as between Dravidian and Indo-Iranian, for example, do not show up in their tree. Despite it not interfering with the reconstruction of young language families that much (i.e. within the last 5000 years), it may affect the reconstruction of macro-families, as we will see.
A more reasoned approach is to look at the vocabulary similarities between languages and ask how plausible they really are. Somebody called 'Ebizur' on the same blog commented on the supposed cognates between Korean and Burushaski:
Another objection might be that language contact is partly responsible for the similarities between geographically neighbouring languages. The authors acknowledge the problem of language contact, but also say that it often does not affect the results: known instances of contact such as between Dravidian and Indo-Iranian, for example, do not show up in their tree. Despite it not interfering with the reconstruction of young language families that much (i.e. within the last 5000 years), it may affect the reconstruction of macro-families, as we will see.
Simon Greenhill and Russell Gray pointed out to me that it gets the structure of some language families wrong. Austronesian has a well-known structure in which the first branches are all in Taiwan, a structure that Jäger and Wichmann's tree fails to recover. One might then wonder why we can trust these results. If the tree fails to accurately recover language families that are only 5000 years old, how can it get families that are tens of thousands of years old?
There are unfortunately some more important problems. An easy-to-miss point in their paper is that in fact the algorithm does not just use distances between word lists to construct the tree; it also uses a second distance measure between languages, namely phonological distance, based on what bigrams occur in each language (pp.3-4):
To calculate the secondary distance measure we represented each doculect as a binary vector representing the presence/absence of bigrams of the 41 ASJP sound classes in the corresponding word lists. The bigram inventory distance between two doculects is then defined as the Jaccard distance between the corresponding vectors...The relative weight of lexical to bigram inventory distances was, somewhat arbitrarily, set to 10:1. In this way it was assured that phylogenetic inference is dominated by the information in the PMI distances, and bigram inventory distances only act as a kind of tie breaker in situations where lexical distances do not provide a detectable signal.
This is important, because the macro-families that they detect are therefore not necessarily reflecting relatedness of vocabulary items, but simply reflect phonological similarity, which could easily be due to language contact. This method was not used in Jäger's PNAS paper, and the authors give no justification for using it here. There is in fact no good reason to use it, if the aim is to push back reconstruction of vocabulary.
It is an interesting, but separate, question whether you can use the sound systems of languages to investigate their history. I replicated that part of their method, taking the ASJP data and bigrams of characters in each word list (although I'm not sure why they used bigrams in particular), and then computed the Jaccard distance between each language. I then made a neighbour-joining tree of the 7000 languages in the data based on this distance measure. The tree is very large, so here is one part of it:
There are some intriguing patterns here, because all of these languages are found in North, South and Central America, and are grouped together here purely because they have similar phoneme inventories. The second group below shows the way that Afro-Asiatic languages such as Berber, Arabic, Aramaic, Amharic and so on cluster together, which are placed with some Eurasian families such as Mongolic, Tungusic and Indo-European languages, perhaps explaining why they were placed with Eurasian languages in Jäger and Wichmann's tree. But there are also some African languages in this group, perhaps reflecting language contact, and some which have no explanation because they are from other continents (such as Algonquin).
The results show a few geographical patterns and a weak sign of clustering by language family, but there is also a lot of noise. This is not surprising, partly because the implementation here is clumsy (a neighbour-joining method, and the use of bigrams rather than all n-grams), but also because nobody normally expects sound systems by themselves to tell us much about language relatedness. I think there may be something worth exploring further - for example why languages in the Americas are similar in their phonological inventories - but the question here is why Jäger and Wichmann use this phonological distance measure, without justification, if it is not reliable for showing how languages are related.
Note too that the vocabulary distance and phonological distance are combined with an arbitrary weighting of 10:1. This means that known language families are recovered with little interference from phonological distance (meaning that it avoids silly results like Algonquin being placed in the Afro-Asiatic family), but beyond that point, where similarity between vocabulary of different language families is minimal, then the phonological distance measure comes into effect. This allows them to get a superficially impressive result: known language families and geographically plausible macro-families. In reality, the result may be more banal: known language families are recovered using one distance measure, but it is unable to reconstruct anything beyond what we already know; and the other distance measure hints at large-scale geographical patterns, but is unable to produce sensible results at the more local level of known language families. And to return to the issue of language contact, their first distance measure may be relatively immune to borrowing, and hence works over a 5000 year time scale; but this does not mean that the phonological distance measure is immune to borrowing, which comes into play at time depths beyond that.
The other main problem with Jäger and Wichmann's method, as I have raised before in my review of Jäger's PNAS paper, is the use of a neighbour-joining algorithm to construct the family tree. Neighbour-joining is the principle that the more similar two things (languages or species) are, the more likely they are to be closely related. To see why this is wrong, consider the three animals below. The two animals that look like mice share a lot of morphological traits in common - they are small, have four legs and a tail, similar skulls, fur, and so on. On a neighbour-joining principle, one would guess that the two mouse-like creatures are closely related, and they are more distantly related to dolphins.
In fact this is wrong: the mouse and the dolphin are most closely related to each other, being placental mammals. The animal on the far left is antechinus, a marsupial that evolved its mouse-like form independently in Australia (famous for its 'suicidal' mating habits, in which the male dies of exhaustion after copulating for fourteen hours).
We know that the mouse and dolphin are more closely related to each other than they are to antechinus despite being superficially more different, because the bodies of animals can change very rapidly, especially when under new selection pressures from the environment; relatively closely related species such as whales and hippos can differ in a large number of traits because whales adapted to life in water. Other traits of animals are much slower-changing, such as the reproductive system, which along with a few other slow-changing traits clearly separate the marsupials from the placental mammals (and using DNA rather than morphological traits makes this clearer). Taking different rates of change into account suggests that the true tree is more like this:
This is perhaps a reason for why Jäger and Wichmann's algorithm gets the structure of Austronesian wrong. It places some Oceanic branches on the outside of the Austronesian tree, perhaps because they have undergone a lot of evolutionary change, analogous to the way that whales underwent rapid change when their ancestors went into the water. In a neighbour-joining method, the amount of change that languages have undergone is confounded with how distantly related languages they are.
It is not just that a neighbour-joining method of constructing a family is inaccurate. In a sense, it gets the whole notion of relatedness wrong. Truly related animals (or languages) are not expected to necessarily be similar overall, and one should be worried if they are: overall similarity is likely to accrue by chance between unrelated species, given enough time (as with the mouse and antechinus), whereas genuine relatedness is detectable in only a few slow-changing traits. In the case of languages, even languages in a well-established family such as Indo-European have only a few words in common between all members, such as words for two and five (as shown in this paper), because most cognates get replaced by new words over time. If the languages in Jäger and Wichmann's tree really are related, there should be specific words that are common to them that can be demonstrated to be slow-changing, rather than showing similarity distributed throughout the entire word list.
To test this, one should Bayesian phylogenetic methods, rather than neighbour-joining based on distances between languages. These methods calculate the probability of trees being true under different models of evolution, and take into account the fact that words evolve at different rates and can get lost entirely. The family trees that you test can also incorporate branch lengths, reflecting the fact that not all species evolve at the same rate.
Bayesian phylogenetics asks what the likelihood of a family tree is, namely with what probability the data would be the way that it is if the hypothesis (the family tree being proposed) were true. If one were to rerun the history of mammals, the probability that we would get exactly the mammals that we actually see on Earth is very, very small; the number of possible mammals that could have evolved is huge, and the species that actually exist are a tiny fraction. But this probability would be even smaller if their family trees had been much different. There are certain family trees which make the evolution of these species more likely, such as a tree which places humans with chimpanzees, although crucially these do not have to be the same as the trees with the fewest changes (the most parsimonious tree, formed by neighbour-joining).
The probability of the data can be calculated for each tree (by considering every possible scenario for how traits, or DNA nucleotides, changed at each node of the tree, and summing over these possible scenarios), and also calculated using different assumptions about how fast- or slow-changing each trait is. Ideally one would then like to check every tree and calculate its likelihood; since there are normally too many possible trees to check, a Markov Chain Monte Carlo method is used to search through trees and sample them according to how likely they are (see John Huelsenbeck's article here on Bayesian phylogenetics).
Bayesian phylogenetics asks what the likelihood of a family tree is, namely with what probability the data would be the way that it is if the hypothesis (the family tree being proposed) were true. If one were to rerun the history of mammals, the probability that we would get exactly the mammals that we actually see on Earth is very, very small; the number of possible mammals that could have evolved is huge, and the species that actually exist are a tiny fraction. But this probability would be even smaller if their family trees had been much different. There are certain family trees which make the evolution of these species more likely, such as a tree which places humans with chimpanzees, although crucially these do not have to be the same as the trees with the fewest changes (the most parsimonious tree, formed by neighbour-joining).
The probability of the data can be calculated for each tree (by considering every possible scenario for how traits, or DNA nucleotides, changed at each node of the tree, and summing over these possible scenarios), and also calculated using different assumptions about how fast- or slow-changing each trait is. Ideally one would then like to check every tree and calculate its likelihood; since there are normally too many possible trees to check, a Markov Chain Monte Carlo method is used to search through trees and sample them according to how likely they are (see John Huelsenbeck's article here on Bayesian phylogenetics).
The data needed to apply this method is either DNA data, or a string of 0's and 1's which represent the presence or absence of traits (e.g. legs, placenta, small skull...). In the case of languages, the approach taken since Russell Gray and Fiona Jordan's pioneering paper in 2000 on Austronesian is to code the presence or absence of cognate classes. For example, main in French and mano in Italian are similar enough that they are likely to be related (or borrowed); hence one can code French and Italian as 1 (meaning they have a word which is part of this cognate class), and English as 0 because it has hand, which is not in this cognate class. English then gets a 1 for the next cognate class (cognates of hand, which exist in Germanic languages), while French and Italian get 0.
To apply this to the ASJP data, one would have to sort words in the data according to classes of likely cognates. As an initial test of this, I used the matrix of likely substitutions that Jäger supplied in his PNAS paper, and computed similarity scores between words using the same alignment algorithm as in his paper, the Needleman-Wunsch algorithm (using the Python package nwalign). A clustering algorithm such as the UPGMA algorithm (implemented in Python in Mattis List's package Lingpy) can then be used which sorts words into clusters, using an arbitrary cut-off point beyond which words are judged to be to dissimilar to be related.
As an example, here are words for 'I/me' in different Indo-European and Austronesian languages, sorted by the cognate groups that the algorithm finds:
Class 1
ene, xina, xine, kinaN, inE, ina, i5a
Class 2
saikin, sak3n, sakon, sak, ak3n, yak3n, aken, tiaq3n, ha77on, ha77in
Class 3
ik, ik3, ix
Class 4
inau, enau, inda7u, inahu, inaku, iau, kinau, kinu, ki5u, Nanu, Nau, nau, axanau, anau, Noua, Nou, nou, inu, ino, inoi, no, nu
Class 5
Eku, ako, qaku, yoku, yaku, yako, iaku, i7aku, yaku7, yako7, aku7, akuh, agu, 53ku, ha7o, wa7u, ia7u, a7u, ga7u, Na7o, ahu, ku, uku, hu, wau, au, auw, lau, ilau, rau, iyau, eyau, yau, dyau, yao, kyau, yaw
These are not the best cognate judgements, but the sound changes in each cognate class are at least quite plausible, such as 'inaku' to 'inda7u' and 'kinau', showing that Jäger and Wichmann's similarity judgement algorithm seems to work. I've heard that using distance measures and clustering in Lingpy in general seems to agree 90% of the time with a human's judgement, which is about as often as humans agree with each other.
More importantly, this method is reproducible and consistent, and avoids the subjectivity of human linguists, one whom Roger Blench once quoted as saying 'I always find more cognates after a good lunch'. It is additionally interesting that you can make the algorithm more 'lumping' or 'splitting' depending on the distance threshold you choose. A higher threshold, the clustering algorithm's equivalent of a good lunch, causes it to merge the above cognate classes into a single cognate class, which may be useful for some purposes such as detecting cognates in large families.
Does this method perform any better than Jäger and Wichmann's method? Unlike their method, you cannot analyse all 6000 languages at the same time, as it is computationally intensive to analyse even one thousand languages using BEAST. I analysed 194 Indo-European languages as an initial test, producing the following tree, where numbers on each node represent the posterior probability of each clade.
It's hard to read and preliminary, but there are some pleasing results. English is placed closest to Frisian and slightly more distantly with Dutch, which is correct according to Glottolog and the consensus among historical linguists. By contrast, Jäger and Wichmann's paper (and Jäger's 2015 paper) gets the position of English wrong, placing it with Scandinavian languages because of Scandinavian loan-words in English. It even does better than Bouckaert et al.'s 2012 paper in Science on Indo-European, which places English as equally related to all West Germanic languages (i.e. equally related to German as it is to Dutch).
The Romance languages also look correct, with Latin and Italian dialects placed as the first branches off, therefore placing the origin of the Romance languages correctly in Italy (which was one of the main success stories of Bouckaert et al.'s paper on the phylogeography of Indo-European). There is a strongly supported clade for Germanic-Romance and then higher up for Germanic-Romance-Celtic, which geographically makes sense (all are the westernmost branches of Indo-European) and is not too different from the clade proposed by Bouckaert et al., namely Romance-Celtic with Germanic on the outside. Greek and Balto-Slavic languages then join this group, which finally join with languages in India. Hittite is disappointingly placed with Albanian and the Balto-Slavic languages, rather than as its own primary branch.
I then analysed a set of mostly Austronesian languages with some Indo-European languages thrown in as well. It recognised that Indo-European and Austronesian were different families (phew), but fails to recover the structure for Austronesian. Further tests on Austronesian languages by themselves also failed to recover a sensible structure for the family, with low posterior probabilities (<10%) on each clade, no matter how lumping or splitting the cognate threshold was.
The results are mixed so far, perhaps because of the nature of the ASJP data (maybe the Austronesian data in particular isn't good enough), and because of the inherent difficulty in cognate-classification. Jäger and Wichmann are presumably trying ways of cognate-coding the data (or have already done so), and many other people interested in automatic cognate-coding have worked with the ASJP data (such as this paper by Hauer and Kondrak, and an ingenious recent paper by Taraka Rama on using convolutional networks for cognate-coding), and of course Mattis List who is the main author of Lingpy.
Despite this, I have not seen discussion (published or otherwise) of automatically detected cognates in the ASJP data that support macro-families. That is the main task in evaluating Jäger and Wichmann's paper, which I think is worth doing given the intriguing geographical patterns that they find. There is ongoing work on building better databases of vocabulary for the world's languages, both in Tübingen (where Jäger is based) and in the Glottobank group at the MPI for the Science of Human History in Jena (a group which two other authors on this blog, Hedvig and Siva, and I are part of), with the aim of pushing back our knowledge of the history of languages further back in time. Jäger and Wichmann's paper has made me more optimistic that these new databases will yield results.
In the mean time, it is worth continuing to analyse the ASJP data using Jäger and Wichmann's method and checking whether their global family tree stands up to Bayesian scrutiny. My attempt at this analysis I will leave to another blog post, especially as I have not done it yet. Is Austro-Tai a valid family? Are the origins of Afro-Asiatic in Eurasia? Is South America a monophyletic clade? Find out in the next instalment. Maybe.
------
Post scriptum
Gerhard Jäger kindly sent a reply to my blog post, with some criticism of my points including the antechinus example, which I post here with his permission.
Dear Jeremy,
Thanks for your thoughtful and fair comments on our paper! Here are replies to some of them. (Everything below reflects my own opinion; Søren might disagree.)
As you know, there was a strict page limit for that proceedings paper, so we couldn't discuss all issues in as much depth as we wanted to. Stay tuned; there will be a follow-up.
A remark on the ASJP data: We only used the 40-item vocabulary lists throughout. For ca. 300 doculects, ASJP has 100-item lists, but we figured using items 41-100 might introduce a bias, so we left them out. Also, ASJP contains quite a few gaps, so in total there are about 36 entries per doculect only. I keep being amazed on how much information you can squeeze out of so few data. :-)
Perhaps the central point: You write:
„There are unfortunately some more important problems. An easy-to-miss point in their paper is that in fact the algorithm does not just use distances between word lists to construct the tree; it also uses a second distance measure between languages, namely phonological distance. […] This is important, because the macro-families that they detect are therefore not necessarily reflecting relatedness of vocabulary items, but simply reflect phonological similarity, which could easily be due to language contact. This method was not used in Jäger's PNAS paper, and the authors give no justification for using it here. There is in fact no good reason to use it, if the aim is to push back reconstruction of vocabulary.“
My apologies if this was easy-to-miss; it is in fact the most important methodological innovation of the paper.
As you also point out, similarities in vocabulary items give enough information to identify language families and their internal structure (with some caveats, of course; borrowings and chance similarities occasionally kick in, but overall this works reasonably well). There is little you can say about trans-family patterns on the basis of vocabulary alone. What I did in my PNAS paper is, in my experience, pretty much the best you can do in this respect. (Longer word lists might help, but I am not very confident in this respect.) There is a lexical signal for Eurasiatic, Austro-Tai, Australian, but that's about it. In fact, if you run the method from my PNAS paper on the entire ASJP, most supra-family groupings have low confidence values and presumably reflect chance similarities more than anything else. (The languages of the Americas and the Papuan languages are lexically extremely diverse.)
This is where the information about phonetic inventories kick in. As you also noticed, this signal is very noisy, and if you do phylogenetic inference with it alone, you get pretty poor phylogenies. The phonetic inventories do carry a deep signal though. Most macro-patterns in our tree reflect similarities in phonetic inventories.
If Atkinson was right in his out-of-Africa paper (http://science.sciencemag.org/content/332/6027/346), sound inventories might carry a very deep phylogenetic signal. I do not want to rule this out a priori. It is equally conceivable though that this is all language contact. Even if so, this is a relevant finding, I think, as it points to prehistoric language contact.
I do not have a firm opinion on this, but my best guess is that the truth is somewhere in the middle, i.e., phonetic inventories carry information both about vertical and about horizontal transmission. Disentangling the two is one of the big challenges for the future.
There is no denying that several groupings in our tree reflect language contact. I commented on this in my PNAS paper in relation to the (probably non-genetic) Sino-Tibetan + Hmong-Mien grouping, but there are certainly many more instances of this kind. The placement of Japanese next to Sino-Tibetan you mention is a case in point.
I suppose (something to explore in the future) that the problems with the internal structure of Austronesian Greenhill and Gray pointed out to you also reflect contact, albeit in an indirect way. Just shooting from the hip: There are many loanwords between the Oceanic branch of Austronesian and Papuan languages. This results in a non-tree-like lexical signal. This effect is not strong enough to pull the affected Austronesian languages out of the Austronesian cluster, or to pull the Papuan languages into the Austronesian cluster, but it leads to a rotation of the Austronesian tree topology in such a way that Oceanic is moved to the periphery and the Taiwanese branches end up in the interior. (This does not explain all problems with the Austronesian tree, but perhaps the most conspicuous one.)
I do not agree with your comments on the phylogenetic algorithms. Neighbor Joining (actually we used Minimum Variance Reduction, but this is a close cousin of Neighbor Joining) is not as good as Bayesian phylogenetic inference (if your data are in the right format to do a Bayesian analysis, that is), but it is a good approximation in many cases. It certainly does not have the inherent bias you describe.
Your example with the mouse, the antechinus and the dolphin is not very well chosen, for several reasons. Neighbor joining (like Maximum Parsimony, Maximum Likelihood any most other phylogenetic inference algorithms) computes an *unrooted* tree. As there is only one unrooted tree topology over three taxa, any algorithm will give you the right result here. So let us, for the sake of the argument, add a shark to the mix. There are three different topologies over four taxa, only one of which is correct.
In your description of the algorithm, distances are calculated on the basis of morphological traits such as „small“, „hase four legs“, „has fur“ etc. This would, in fact, lead to the wrong topology
((shark, dolphin),(mouse,antechinus))
But the same would happen if you arrange your morphological traits in a character matrix and do character-based inference:
small four_legs tail fur fin lives_in_water
mouse 1 1 1 1 0 0
antechinus 1 1 1 1 0 0
dolphin 0 0 0 0 1 1
shark 0 0 0 0 1 1
Any character-based phylogenetic inference algorithm will give you the same topology, simply because there are no mutations separating mouse and antechinus, and likewise none separating dolphin and shark.
The deeper problem here is that we have *convergent evolution*, i.e. all those characters evolved twice, due to natural selection. Standard phylogenetic algorithms are not really applicable with those data as they rely on a neutral model of evolution, i.e., the absence of selection.
If you would compare those four species on the basis of their DNA, Neighbor Joining would undoubtedly give you the correct topology, just like character-based methods.
(There is a still unpublished paper by Johann-Mattis List and me where we, among other things, discuss the pros and cons of various phylogenetic algorithms: http://www.sfs.uni-tuebingen.de/~gjaeger/publications/jaegerListOxfordHandbook.pdf)
As you point out, to perform Bayesian phylogenetic inference you need data in a character matrix format. As there are no expert cognacy judgments so far for most language families, doing this for data beyond well-studied families is a challenge. Distance-based phylogenetic inference (such as Neighbor Joining or Minimum Variance Reduction) is one way to circumvent this problem. Using automatic methods to bring ASJP data into character format, as you suggest, is another option – one we are currently exploring as well. In this connection you might find this manuscript (also co-authored by Mattis and me: http://www.sfs.uni-tuebingen.de/~gjaeger/publications/svmPaper.pdf) interesting. I am happy to share more information about this sub-task off-line.
To conclude for today: With our method we come up with an automatically inferred tree for more than 6,000 doculects (representing ca. 4,000 languages with separate ISO codes – two thirds of global linguistic diversity) which has a Generalized Quartet Distance of 0.046 to the Glottolog expert tree. The challenge is on: Can we do better than this?
To apply this to the ASJP data, one would have to sort words in the data according to classes of likely cognates. As an initial test of this, I used the matrix of likely substitutions that Jäger supplied in his PNAS paper, and computed similarity scores between words using the same alignment algorithm as in his paper, the Needleman-Wunsch algorithm (using the Python package nwalign). A clustering algorithm such as the UPGMA algorithm (implemented in Python in Mattis List's package Lingpy) can then be used which sorts words into clusters, using an arbitrary cut-off point beyond which words are judged to be to dissimilar to be related.
As an example, here are words for 'I/me' in different Indo-European and Austronesian languages, sorted by the cognate groups that the algorithm finds:
Class 1
ene, xina, xine, kinaN, inE, ina, i5a
Class 2
saikin, sak3n, sakon, sak, ak3n, yak3n, aken, tiaq3n, ha77on, ha77in
Class 3
ik, ik3, ix
Class 4
inau, enau, inda7u, inahu, inaku, iau, kinau, kinu, ki5u, Nanu, Nau, nau, axanau, anau, Noua, Nou, nou, inu, ino, inoi, no, nu
Class 5
Eku, ako, qaku, yoku, yaku, yako, iaku, i7aku, yaku7, yako7, aku7, akuh, agu, 53ku, ha7o, wa7u, ia7u, a7u, ga7u, Na7o, ahu, ku, uku, hu, wau, au, auw, lau, ilau, rau, iyau, eyau, yau, dyau, yao, kyau, yaw
These are not the best cognate judgements, but the sound changes in each cognate class are at least quite plausible, such as 'inaku' to 'inda7u' and 'kinau', showing that Jäger and Wichmann's similarity judgement algorithm seems to work. I've heard that using distance measures and clustering in Lingpy in general seems to agree 90% of the time with a human's judgement, which is about as often as humans agree with each other.
More importantly, this method is reproducible and consistent, and avoids the subjectivity of human linguists, one whom Roger Blench once quoted as saying 'I always find more cognates after a good lunch'. It is additionally interesting that you can make the algorithm more 'lumping' or 'splitting' depending on the distance threshold you choose. A higher threshold, the clustering algorithm's equivalent of a good lunch, causes it to merge the above cognate classes into a single cognate class, which may be useful for some purposes such as detecting cognates in large families.
It's hard to read and preliminary, but there are some pleasing results. English is placed closest to Frisian and slightly more distantly with Dutch, which is correct according to Glottolog and the consensus among historical linguists. By contrast, Jäger and Wichmann's paper (and Jäger's 2015 paper) gets the position of English wrong, placing it with Scandinavian languages because of Scandinavian loan-words in English. It even does better than Bouckaert et al.'s 2012 paper in Science on Indo-European, which places English as equally related to all West Germanic languages (i.e. equally related to German as it is to Dutch).
The Romance languages also look correct, with Latin and Italian dialects placed as the first branches off, therefore placing the origin of the Romance languages correctly in Italy (which was one of the main success stories of Bouckaert et al.'s paper on the phylogeography of Indo-European). There is a strongly supported clade for Germanic-Romance and then higher up for Germanic-Romance-Celtic, which geographically makes sense (all are the westernmost branches of Indo-European) and is not too different from the clade proposed by Bouckaert et al., namely Romance-Celtic with Germanic on the outside. Greek and Balto-Slavic languages then join this group, which finally join with languages in India. Hittite is disappointingly placed with Albanian and the Balto-Slavic languages, rather than as its own primary branch.
I then analysed a set of mostly Austronesian languages with some Indo-European languages thrown in as well. It recognised that Indo-European and Austronesian were different families (phew), but fails to recover the structure for Austronesian. Further tests on Austronesian languages by themselves also failed to recover a sensible structure for the family, with low posterior probabilities (<10%) on each clade, no matter how lumping or splitting the cognate threshold was.
The results are mixed so far, perhaps because of the nature of the ASJP data (maybe the Austronesian data in particular isn't good enough), and because of the inherent difficulty in cognate-classification. Jäger and Wichmann are presumably trying ways of cognate-coding the data (or have already done so), and many other people interested in automatic cognate-coding have worked with the ASJP data (such as this paper by Hauer and Kondrak, and an ingenious recent paper by Taraka Rama on using convolutional networks for cognate-coding), and of course Mattis List who is the main author of Lingpy.
Despite this, I have not seen discussion (published or otherwise) of automatically detected cognates in the ASJP data that support macro-families. That is the main task in evaluating Jäger and Wichmann's paper, which I think is worth doing given the intriguing geographical patterns that they find. There is ongoing work on building better databases of vocabulary for the world's languages, both in Tübingen (where Jäger is based) and in the Glottobank group at the MPI for the Science of Human History in Jena (a group which two other authors on this blog, Hedvig and Siva, and I are part of), with the aim of pushing back our knowledge of the history of languages further back in time. Jäger and Wichmann's paper has made me more optimistic that these new databases will yield results.
In the mean time, it is worth continuing to analyse the ASJP data using Jäger and Wichmann's method and checking whether their global family tree stands up to Bayesian scrutiny. My attempt at this analysis I will leave to another blog post, especially as I have not done it yet. Is Austro-Tai a valid family? Are the origins of Afro-Asiatic in Eurasia? Is South America a monophyletic clade? Find out in the next instalment. Maybe.
------
Post scriptum
Gerhard Jäger kindly sent a reply to my blog post, with some criticism of my points including the antechinus example, which I post here with his permission.
Dear Jeremy,
Thanks for your thoughtful and fair comments on our paper! Here are replies to some of them. (Everything below reflects my own opinion; Søren might disagree.)
As you know, there was a strict page limit for that proceedings paper, so we couldn't discuss all issues in as much depth as we wanted to. Stay tuned; there will be a follow-up.
A remark on the ASJP data: We only used the 40-item vocabulary lists throughout. For ca. 300 doculects, ASJP has 100-item lists, but we figured using items 41-100 might introduce a bias, so we left them out. Also, ASJP contains quite a few gaps, so in total there are about 36 entries per doculect only. I keep being amazed on how much information you can squeeze out of so few data. :-)
Perhaps the central point: You write:
„There are unfortunately some more important problems. An easy-to-miss point in their paper is that in fact the algorithm does not just use distances between word lists to construct the tree; it also uses a second distance measure between languages, namely phonological distance. […] This is important, because the macro-families that they detect are therefore not necessarily reflecting relatedness of vocabulary items, but simply reflect phonological similarity, which could easily be due to language contact. This method was not used in Jäger's PNAS paper, and the authors give no justification for using it here. There is in fact no good reason to use it, if the aim is to push back reconstruction of vocabulary.“
My apologies if this was easy-to-miss; it is in fact the most important methodological innovation of the paper.
As you also point out, similarities in vocabulary items give enough information to identify language families and their internal structure (with some caveats, of course; borrowings and chance similarities occasionally kick in, but overall this works reasonably well). There is little you can say about trans-family patterns on the basis of vocabulary alone. What I did in my PNAS paper is, in my experience, pretty much the best you can do in this respect. (Longer word lists might help, but I am not very confident in this respect.) There is a lexical signal for Eurasiatic, Austro-Tai, Australian, but that's about it. In fact, if you run the method from my PNAS paper on the entire ASJP, most supra-family groupings have low confidence values and presumably reflect chance similarities more than anything else. (The languages of the Americas and the Papuan languages are lexically extremely diverse.)
This is where the information about phonetic inventories kick in. As you also noticed, this signal is very noisy, and if you do phylogenetic inference with it alone, you get pretty poor phylogenies. The phonetic inventories do carry a deep signal though. Most macro-patterns in our tree reflect similarities in phonetic inventories.
If Atkinson was right in his out-of-Africa paper (http://science.sciencemag.org/content/332/6027/346), sound inventories might carry a very deep phylogenetic signal. I do not want to rule this out a priori. It is equally conceivable though that this is all language contact. Even if so, this is a relevant finding, I think, as it points to prehistoric language contact.
I do not have a firm opinion on this, but my best guess is that the truth is somewhere in the middle, i.e., phonetic inventories carry information both about vertical and about horizontal transmission. Disentangling the two is one of the big challenges for the future.
There is no denying that several groupings in our tree reflect language contact. I commented on this in my PNAS paper in relation to the (probably non-genetic) Sino-Tibetan + Hmong-Mien grouping, but there are certainly many more instances of this kind. The placement of Japanese next to Sino-Tibetan you mention is a case in point.
I suppose (something to explore in the future) that the problems with the internal structure of Austronesian Greenhill and Gray pointed out to you also reflect contact, albeit in an indirect way. Just shooting from the hip: There are many loanwords between the Oceanic branch of Austronesian and Papuan languages. This results in a non-tree-like lexical signal. This effect is not strong enough to pull the affected Austronesian languages out of the Austronesian cluster, or to pull the Papuan languages into the Austronesian cluster, but it leads to a rotation of the Austronesian tree topology in such a way that Oceanic is moved to the periphery and the Taiwanese branches end up in the interior. (This does not explain all problems with the Austronesian tree, but perhaps the most conspicuous one.)
I do not agree with your comments on the phylogenetic algorithms. Neighbor Joining (actually we used Minimum Variance Reduction, but this is a close cousin of Neighbor Joining) is not as good as Bayesian phylogenetic inference (if your data are in the right format to do a Bayesian analysis, that is), but it is a good approximation in many cases. It certainly does not have the inherent bias you describe.
Your example with the mouse, the antechinus and the dolphin is not very well chosen, for several reasons. Neighbor joining (like Maximum Parsimony, Maximum Likelihood any most other phylogenetic inference algorithms) computes an *unrooted* tree. As there is only one unrooted tree topology over three taxa, any algorithm will give you the right result here. So let us, for the sake of the argument, add a shark to the mix. There are three different topologies over four taxa, only one of which is correct.
In your description of the algorithm, distances are calculated on the basis of morphological traits such as „small“, „hase four legs“, „has fur“ etc. This would, in fact, lead to the wrong topology
((shark, dolphin),(mouse,antechinus))
But the same would happen if you arrange your morphological traits in a character matrix and do character-based inference:
small four_legs tail fur fin lives_in_water
mouse 1 1 1 1 0 0
antechinus 1 1 1 1 0 0
dolphin 0 0 0 0 1 1
shark 0 0 0 0 1 1
Any character-based phylogenetic inference algorithm will give you the same topology, simply because there are no mutations separating mouse and antechinus, and likewise none separating dolphin and shark.
The deeper problem here is that we have *convergent evolution*, i.e. all those characters evolved twice, due to natural selection. Standard phylogenetic algorithms are not really applicable with those data as they rely on a neutral model of evolution, i.e., the absence of selection.
If you would compare those four species on the basis of their DNA, Neighbor Joining would undoubtedly give you the correct topology, just like character-based methods.
(There is a still unpublished paper by Johann-Mattis List and me where we, among other things, discuss the pros and cons of various phylogenetic algorithms: http://www.sfs.uni-tuebingen.de/~gjaeger/publications/jaegerListOxfordHandbook.pdf)
As you point out, to perform Bayesian phylogenetic inference you need data in a character matrix format. As there are no expert cognacy judgments so far for most language families, doing this for data beyond well-studied families is a challenge. Distance-based phylogenetic inference (such as Neighbor Joining or Minimum Variance Reduction) is one way to circumvent this problem. Using automatic methods to bring ASJP data into character format, as you suggest, is another option – one we are currently exploring as well. In this connection you might find this manuscript (also co-authored by Mattis and me: http://www.sfs.uni-tuebingen.de/~gjaeger/publications/svmPaper.pdf) interesting. I am happy to share more information about this sub-task off-line.
To conclude for today: With our method we come up with an automatically inferred tree for more than 6,000 doculects (representing ca. 4,000 languages with separate ISO codes – two thirds of global linguistic diversity) which has a Generalized Quartet Distance of 0.046 to the Glottolog expert tree. The challenge is on: Can we do better than this?









Hi Jeremy (and Gerhard)
ReplyDeleteThis is a great discussion of very interesting research, and I'm happy to see some of my own recent work being picked up on, even if not explicitly.
Jeremy, you write about the use of bigrams, "This method was not used in Jäger's PNAS paper, and the authors give no justification for using it here". Gerhard refers to it as “the most important methodological innovation of the paper”.
The justification and the antecedent for this approach, I would guess, is a paper by Jayden Mackiln-Cordes and me, published after Gerhard’s PNAS paper and before the EvoLang paper, and presented at a conference hosted by Gerhard's research group in November 2015. It's available here:
https://www.academia.edu/20320642/High-Definition_Phonotactics_Reflect_Linguistic_Pasts
http://dx.doi.org/10.15496/publikation-8609
In that paper we show that simple bigram phonotactics contains phylogenetic signal. Interestingly however, we demonstrated that using binary bigram presence/absence scores recovers poor phylogenetic signal at best, whereas richer, continuous probabilistic data does recover good signal, at least in shallow genealogical groups.
I'll be interested to read discussion of the EvoLang results in relation to our own findings in the follow-up paper Gerhard has foreshadowed here.
Very best, Erich.
Hi Erich - Thanks very much for the interesting paper, I will have a look at it and also describe it in a follow-up post (with your permission). I think that is the main thing to continue to explore in the ASJP - if as Gerhard says the signal for macro-families is mainly from phonological similarity, then we need to work out what is going on there (how much is contact for example).
DeleteHi Erich,
ReplyDeleteThanks for the reminder. Yes, you are right, there is some previous work on phonological inventories and phylogenetics, including your paper (Rama and Borin 2015 also look at bigram inventory distances: Rama, Taraka, and Lars Borin. "Comparative evaluation of string similarity measures for automatic language classification." Sequences in Language and Text 69 (2015): 171). This topic definitely merits some more thorough discussion in a longer paper.
With "methodological innovation" I was referring to the idea of combining lexical and phonetic information during phylogenetic inference.
Cheers, Gerhard